Standardizing datasets: Z-Score

A z-score is the difference between the observed and expected (mean) value of a variable, standardized by the standard deviation. You can calculate two kinds of z-scores in SpaceStat: a z-score using the instantaneous or time-slice mean, and one using the time-weighted mean over the entire dataset time range.

Z-scores are distributed approximately normally, with a mean of 0 and a variance of 1.0. An added wrinkle in SpaceStat is that the z-score is taken at a specified time or range and the new dataset has that time stamp.

Many statistics do not use raw data but standardized versions of the datasets. When you ask for an analysis requiring a z-score, SpaceStat will calculate it for you automatically during the other calculations. You can also create z-scores of your datasets separate from any other statistical method.

The Z-score equations

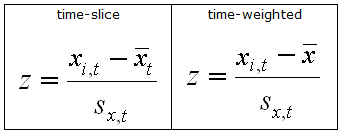
• xi,t is the value of the variable x observed at location i at time t

• xt is the mean of variable x at timet over all locations

• x is the mean of variable x over all times

• sx,t is the standard deviation of variable x at timet