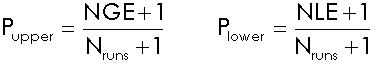Calculating Monte Carlo P-values
The p-value is the relative ranking of the test statistic among the sample values from the Monte Carlo randomization. You can calculate p-values to see whether observed values are unusually large or small for the null distribution. This calculation compares the observed value to the upper and the lower tails of the null distribution.
|
|
Nruns is the total number of Monte Carlo simulations |
|
NGE is the number of simulations for which the statistic was greater than or equal to the observed statistic |
|
|
NLE is the number of simulations for which the statistic was lower than or equal to the observed statistic |
|
|
One (1) is added to the numerator and denominator because the observed statistic is included in the reference distribution. |
How many randomizations?
As you can see in the equations above, the number of randomizations sets the minimum p-value you can resolve. There is a trade-off between precision and calculation time. More randomizations are slower, but the p-value is more precise.
For instance, if you do 20 randomizations, the minimum possible p-value is 0.05. If you use the Simes correction, you may want to increase the number of randomizations, as the initial Monte Carlo p-values may be raised to adjust for multiple comparisons.