Besag and Newell's l

Besag and Newell's method calculates two statistics: l is the local statistic, the number of regions required for the window centered over an individual region to contain k cases. To evaluate whether the k cases form a cluster, the method looks to see whether the number of cases in the window is unlikely for the window's population at risk.

The null hypothesis is that there is no clustering, so that a common Poisson disease rate exists across the study area. Thus, the case count inside the window should be proportional to the population at risk, otherwise the null hypothesis can be rejected. Following Besag and Newell (1991), the null spatial model is that cases are distributed among the areas in the study proportional to population size and with a common disease rate. SpaceStat calculates a probability for l under the null spatial model.

 

This expression calculates the probability that l has reached or exceeded the value predicted by the null hypothesis (L). It is 1 minus the probability that l is less than L, i.e., the probability that there are fewer than k cases in the area. The probability of 0 through k-1 cases is found by summing the Poisson term from x = 0 to x = k-1. Lambda, ( 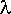), is the average or expected case count, the average or expected disease frequency multiplied by the population-at-risk. The term e indicates the exponential function.

When you perform a Besag and Newell analysis, SpaceStat will calculate l and its significance for all clusters. It will list all clusters that have a probability less than the significance level you specify, alpha. The default alpha is 0.05.