Exceedance of Thresholds in Disparity

In some situations, such as the prostate cancer mortality example shown in Goovaerts et al. 2007, the disparity between rates is so large and systematic that two-tailed tests primarily serve to confirm an obvious pattern.  To further explore patterns in disparities, SpaceStat incorporates techniques developed in this paper to look at exceedances of specific thresholds of change in both absolute and relative differences in rates.   Note that these tests are again set up in a way that follows the CDC's suggested standard approach, so you can only identify positive threshold values.

One-tailed test for Absolute Disparity (Rate Differences)

In the example described above, the standard two-tailed test (testing whether one set of rates differs from another, in either direction) simply confirms a pattern that is readily apparent when prostate cancer rates for black and white males are displayed in county geography maps.  When differences are this strong, it is often more interesting to test whether disparities exceed particular thresholds, symbolized by .   Exceedance of a particular threshold of differences between absolute disparity values (abbreviated as RD, for Rate Difference) can be tested in SpaceStat using the following one-tailed test:

 

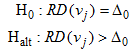
For example, setting =10 would lead to the identification of counties where the black male mortality rate exceeds the rate for white males by 10 deaths/100,000 people (these analyses were done on cancer rates with a 100,000 multiplier).  Goovaerts et al. (2007) modified the absolute (RD)  and relative (rate ratio, or RR) disparity statistics to allow this type of hypothesis test.  The revised formula for the absolute disparity statistic is:

 

One-tailed Test for Relative Disparity (Rate Ratios)

Similarly, the relative difference in rates can be evaluated with a one-sided test to evaluate the following hypothesis:

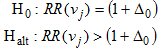
where the disparity threshold, , is now expressed as a proportion.  Thus, this test allows you to set at 0.2, and evaluate whether the mortality rate for black males is significantly greater than 120% of the rate for white males.  The statistic for relative rates is as follows:

 

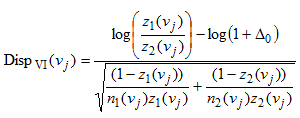
Significance Values for the One-sided Tests

The significance of the two disparity statistics shown above is assessed using the following procedure, where G(.) is the cumulative probability distribution of the standard normal variable.

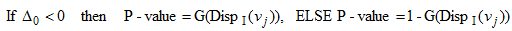
To see how to fill out the pages in the task manager to calculate disparity statistics, click here.