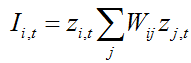Local Moran: Statistic

Ho	There is no association between the value observed at a location and values observed at nearby sites, values of Ii,t are close to zero.
Ha	Nearby sites have either similar or dissimilar values, Ii,t is large and either positive or negative.

Test statistic

Spatial association can be evaluated by comparing matrices of similarity where one matrix expresses spatial similarity (for example, a contiguity or spatial weights matrix) and the other expresses similarity of disease frequency values. Spatio-temporal association can be evaluated by examining the pattern in time to the pattern in values. The Local Moran statistic is based on the gamma index, a general index of matrix association (Anselin 1995).

	zi,t is the z-score standardized dataset being tested for region i at time t.
	zj,t is the z-score standardized dataset for region j at time t. For the univariate Local Moran, zi,t and zj,t refer to the same dataset. For bivariate Moran, they are two separate datasets or a single dataset at two time points (for that replace t with t +D in the formula).
	wij is a spatial weight set denoting the strength of connection between areas i and j.

The Local Moran statistic Ii,t will be positive when values at neighboring locations are similar, and negative if they are dissimilar. SpaceStat evaluates the significance of Local Moran statistic values with Monte Carlo randomizations, using conditional randomization.

The impact of missing values in Local Moran analyses

The spatial weight sets created by adjacency evaluations are independent of any values of datasets associated with the geography, including missing values.  Thus, if you have a dataset with missing values, calculations of the Local Moran statistics will be based on only those neighboring locations with data.  Because the statistics are evaluated for significance with Monte Carlo randomizations (i.e, the differences in the distribution of observed statistic values can influences whether a particular value is judeged as "rare", removing one or more locations from a geography (thus creating missing values) can change results for all locations.  You might observe this if you decide that a value or two represent outliers in your data, and re-run an analysis using missing values instead of the recorded ones.  You will find that results for locations close to the one where missing values now occur change, but results for other locations may change as well due to the change in the overall distribution of Ii,t .