About Poisson Geographically Weighted Regression

Poisson geographically weighted regression is a local form of generalized linear models that assumes that your data follow a Poisson distribution.  This distribution describes the probability of events occurring in time or space when the pattern of these occurrences is random, and is often a good fit for count and rate data.  With Poisson regression, you are building a model to estimate a count or rate using relationships between your independent (predictor) variable(s) and the expected value of your Poisson variable.  Example applications include models to predict counts of the number of people visiting a hospital emergency room at different times of day, or to predict rates, such as death rate (count of deaths divided by person-years) from independent data on contaminant concentrations.  Independent variables in a Poisson regression can be continuous and/or categorical, and you can also include interaction effects and non-geographic weight variables in your model.  Note however that some combinations of categorical variables lead to overspecified models, so read that page so that you know what to avoid when defining your model.  Assumptions of Poisson regression models include (1) independent observations; and (2) independent variables are linearly related to the log of the dependent variable.

The Poisson distribution

A Poisson random variable has a probability density function, f(y), that can be described by the following formula:

Here the parameter lambda is the estimated value of Y, e is the natural log, and the denominator of the equation is y factorial (!), or yi multiplied by (yi - 1), (yi - 2),... 2, 1.  

The shape of the Poisson distribution varies with the expected value per interval (in space or time) of occurrences of the event that is being counted.  Small expected values, such as 1, show a highly skewed distribution, while distributions for higher expected values appear more symmetrical.  This pattern is illustrated below for three datasets with expected values per interval of 1 (blue), 2 (red), and 4 (orange). Recall that the values that can be observed are all integers, so consider the lines connecting the points in the figure below as just a way to visualize the shape of the distribution; they do not indicate a continuous function.

A key characteristic of this distribution is that it's mean and variance are equal, so this is an important first check to apply to your data to help you decide if a Poisson model would be appropriate.  In addition to this check, data that can be characterized with a Poisson distribution have several traits that makes applying linear regression inappropriate.  First, their distribution may be skewed towards small values, as described above and shown in the figure.  For example, this tool is often applied to counts of territorial animal species, where the number of individuals observed at a count location is usually zero or one because territory owners keep others out of the defended space.  However, a binary variable (as used in GWR logistic regression) would not be appropriate, because where individuals interact in space, like at territory boundaries, you may record counts of 2, 3, 4, and so on.  A second characteristic of data for which a Poisson distribution provides a better fit than traditional regression (Gaussian) is non-symmetric distribution of errors.  The Poisson distribution takes only positive values, while negative values are fine in simple linear regression.  Finally, the variance of a Poisson distribution increases as the mean increases, violating the simple linear regression assumption of homoscedasticity.

A general equation for GWR Poisson regression

The general equation for Poisson regression uses a Poisson probability distribution for the individual dependent variable observations.  The equation differs from traditional regression in that the left hand side is the logarithm of the expected value (or mean, symbolized as 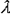) of the dependent variable’s response.  Note that this is the same expected value that parameterizes the Poisson distribution function, as illustrated in the figure above.

Output from Aspatial Poisson regression

SpaceStat output from GWR Poisson regression includes regression coefficients and p-values for individual terms in the model.  The output is described in more detail here, including examples from the SpaceStat log view.

To find out more about how GWR Poisson regression is implemented in SpaceStat, click here.

To skip the details and learn about how to perform Poisson regression, click here.