Aspatial Logistic Regression Output
For logistic regression, SpaceStat presents the parameter estimates, parameter standard errors and p-values (using a chi-squared distribution). In addition, the output includes the parameter odds ratio along with odds ratio confidence intervals.
Here, we will show the output from a new model focused on predicting lung cancer risk in females in western counties. Recall that as described in the "About" page for logistic regression, we need to use a dependent variable that is binary (takes a numeric "code" value of 1 or 0). So, for the logistic model we have converted a continuous lung cancer risk dataset to a binary dataset (F_LUNG_ABOVE_26) by assigning a 1 to all observations with a risk of 26 or higher (e.g., 26 cases per 100,000 people, roughly the median value for this dataset), and 0 to all lower risks observations. We also have a new independent variable, "SmokevrF", which is the percent of females in the county that have ever smoked, and two of the same independent variables from our Cervix cancer example in the "Perform" page, "PoorCat", a categorical version of the proportion of the population with income below the federal poverty level, and MDratio, the ratio of population size to the number of doctors in each county. In this model, we have not included a squared or interaction term, and have chosen the "medium" category in PoorCat as our reference value, with Reference cell as our Parameterization type.

Next, on the settings page, we chose "logistic" as our model type rather than "linear". The only other change in how we performed the logistic regression compared to the linear cervix cancer example is that we added the word "Logistic" to the model title and to the name of the output folder to help us differentiate them from models and output using the other two model types.
Summary of the model run
After clicking to the run method page and then selecting "Run", we see the following output in the log view, beginning with the summary of the model run.

Fit and significance of the model as a whole
Below the review of the model run information, SpaceStat presents the summary of the predictive ability and significance of the model as a whole for the first time period. The dataset described here only includes one time period, but if you analyzed a set with several time intervals, you would see output for each period.
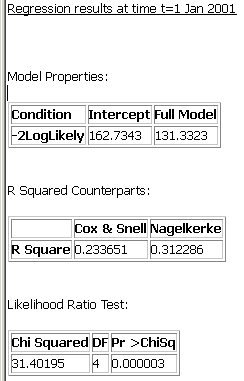
The first table in the output for logistic regression presents the -2Log-Likelihood table, which plays the same role as the sum of squares in linear regression. The first data column in this table shows the value for the Intercept only model, which is similar to the total sum of squares in linear regression; the second data column shows the result for the Full model, which is akin to linear regression's residual sum of squares. The difference between these is used in a Likelihood Ratio test (the third small table shown in the output, above) to determine the significance of the overall model; the p-value for this test is determined from a chi-squared distribution.
Like the model R-squared and adjusted R-squared values in aspatial linear regression, output for logistic regression includes two measures of the strength of the model's predictive ability: the Cox & Snell and Nagelkerke R-squared values. Thus, the results shown here indicate that our model does a reasonable job (with room for improvement) of predicting the log-odds of a county having a lung cancer rate above our threshold, with fit values of 0.23 (Cox and Snell) and 0.31 (Nagelkerke). The Likelihood Ratio test (bottom table) is highly significant, with a p-value of 0.000003 (note that p-values in regression output are reported as "0.0" if they are smaller than 0.000001).
Significance of individual model parameters
The next table in the output for aspatial logistic regression provides the parameter estimates, standard errors, p-values, odds ratios, and 95% Confidence Intervals (C.I.) for each parameter in the model. See the implementation page for a description of how the P-values are derived. Note that as described in the page on categorical variables in regression, a parameter is estimated for each level of a categorical variable, except for the level that is chosen as the reference value. In SpaceStat, the Odds ratios for categorical variables are presented relative to the category chosen as the reference value, so if, for example, you chose the lowest category as your reference value, they may appear unusually large if you are used to interpreting output from other software programs that calculate odd relative to the "mean" category.

This p-value represents the smallest level of significance that would lead to rejection of the null hypothesis that the parameter estimate equals zero. Similar to what we found in the linear regression output, here the intercept and the two continuous variables are significant, with the smoking-related variable having the highest p-value. Neither of the parameter estimates for our categorical variable, PoorCat, was signficant. The next column to the right of the p-value shows the Odds ratio, which is the regression parameter exponentialized. The 95% Confidence Intervals are obtained from the regression parameters' standard error.
Table of correlation coefficients
Finally, the last table produced as part of the output for aspatial logistic regression shows the correlation coefficient for each pair of numeric variables in your model. This is helpful for understanding how different independent variables are related, and can be used to identify terms that could be dropped from the model due to high correlation with other terms (colinearity).

In this example, there is a only a 0.22 correlation between MDratio and SmokevrF; this level of relationship would likely not raise the "red flag" of colinearity.
Note that these values may differ from correlation coefficients presented in the graph statistics window due to the effect of missing values. In the case of the regression model, the correlation will not include data from ANY of the variables at observations where one or more value is missing, while only missing values in the two datasets being compared will influence the correlation coefficient in the graph statistics window in a scatter plot.









